قضیه‌ی Kolmogorov و شبکه‌های عصبی

وقتی Minsky و Papert در سال ۱۹۶۹ کتاب معروف خود پرسپترون‌ها را نوشتند و در آن به نقد و بررس پرسپترون‌ها و نقاط ضعف و قدرت آن‌ها پرداختند نشان دادند که پرسپترون قادر به یادگیری و تخمین توابع غیر خطی نیست. اما آن‌ها این احتمال را که شبکه‌های چند لایه می‌توانند عمل‌کرد بهتری ارائه کنند باز گذاشتند. البته تقریباً بیست سال طول کشید تا کارایی شبکه‌های عصبی چندلایه اثبات شود.

مبانی نظری شبکه‌های عصبی feedforward اولین بار توسط Kolmogorov ارائه شد. او برای اولین بار نشان داد که یک تابع پیوسته از n متغیر، f(x₁, x₂, x₃,...,x_n)، می‌تواند به مجموع توابع یک متغیره نگاشت شود. Andrey Nikolaevich Kolmogorov ریاضی‌دان نابغه‌ی روسی در سال ۱۹۵۸ در یک مقاله قضیه‌ی زیر را اثبات کرد:   

قضیه: به ازای هر n≥2، وجود دارد توابع حقیقی پیوسته‌ی در بازه‌ی بسته‌ی ، به صورتی که هر تابع حقیقی پیوسته‌ی در فضای n بعدی را می‌توان به شکل زیر بازنمایی کرد:

که در آن یک تابع حقیقی پیوسته‌ است.

به عنوان مثال برای n=3 با قرار دادن:

خواهیم داشت:

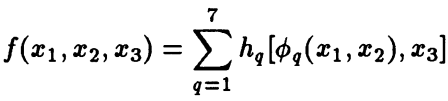
البته قبل از آن، در سال ۱۹۵۷، V.I. Arnol'd نشان داده بود که هر تابع پیوسته‌ از سه متغیر می‌تواند به صورت مجموع هفت تابع به شکلی که در بالا نشان داده شده بازنمایی شود و Kolmogorov آن را به هر تابع n متغیره بسط داد.

کشف عظیم Kolmogorov توسط سایر دانشمندان بهبود یافته و تکمیل شد. Lorentz در سال ۱۹۶۶ نشان داد که توابع می‌توانند با فقط یک تابع جایگزین شوند. در پی آن Sprecher در سال ۱۹۶۵ توابع را با جایگزین کرد که در آن مقدار ثابت بوده و توابع یکنوای صعودی وابسته به کلاس هستند.

در سال ۱۹۸۷، Hecht-Nielsen قضیه‌ی بازنمایی اصلاح شده توسط Sprecher را برای شبکه‌های عصبی دوباره فرموله کرد. به این صورت که هر تابع پیوسته‌ی تعریف شده در فضای n بعدی را می‌توان با یک شبکه‌ی سه لایه با تعداد 2n+1 نورون در لایه‌ی پنهان پیاده‌سازی کرد. در این شبکه توابع به عنوان توابع انتقال از لایه‌ی اول به لایه پنهان و به عنوان تابع انتقال از تمام واحد‌های لایه‌ی پنهان به یک واحد خروجی استفاده می‌شود.

با این اصلاحات با استفاده از قضیه‌ی Kolmogorov اثبات شد که یک شبکه‌ی سه لایه می‌تواند هر مسئله‌ی تشخیص الگو را طبقه‌بندی کند. طرفداران پرسپترون چند لایه در دهه‌ی 80 برای توجیه موفقیت‌های خود به قضیه‌ی Kolmogorov استناد می‌کردند. اغلب این استناد‌ها به قضیه‌ی اصلاح شده توسطLorentz انجام می‌شد. Kolmogorov یک قضیه‌ی امکان نظری مهم را ارائه می‌دهد اما موفقیت‌های به دست آمده را نمی‌تواند توضیح دهد. در آن سال‌ها این سؤال مطرح بود که آیا موفقیت‌های بدست آمده برای شبکه‌های پرسپترون چند لایه در حل مسائل گوناگون ناشی از قابلیت‌های عمیق و اساسی این شبکه‌ها است یا اینکه صرفاً ناشی از گزارش‌های انتخاب شده و انتخاب تصادفی مسئاله‌هاست. در سال ۱۹۸۹ بود که Kurt Hornik به اینگونه سؤالات پاسخ داد. او نشان داد که یک شبکه‌ی چندلایه‌ی feedforward می‌تواند هر تابع مورد نظر را با هر درجه از دقت مورد نظر تقریب بزند به شرطی که تعداد کافی از واحد‌های پنهان موجود باشد. این نتایج شبکه های چند لایه‌ی feedforward را به عنوان یک کلاس تقریب جهانی مطرح کرد. به این ترتیب، شکست در برنامه‌ها را می‌توان به یادگیری ناکافی، تعداد ناکافی واحدهای پنهان یا وجود یک رابطه‌ی تصادفی به جای یک رابطه‌ی قطعی بین ورودی و هدف نسبت داد.

قضیه‌ی Kolmogorov که در ابتدا به عنوان یک قضیه در ریاضیات مطرح شده بود به عنوان مبنایی برای اثبات توانایی‌های شبکه‌های پرسپترون چندلایه به خدمت گرفته شد. بر این اساس می‌توان این قضیه را یکی از ارکان اساسی پیشرفت و توسعه‌ی شبکه‌های عصبی مصنوعی و در پی آن یادگیری عمیق دانست. امروزه دانشمندان ریاضیات، علوم کامپیوتر و هوش مصنوعی همچنان سعی در انجام اصلاحاتی در این قضیه دارند تا بتوانند بر اساس آن به پیشرفت‌های بیشتری در یادگیری عمیق دست پیدا کنند.