معماری اصلی شبکه‌های عصبی بازگشتی

بسیاری از معماری‌های شبکه‌های عصبی، مثل ماشین بولتزمن محدود شده، پرسپترون چندلایه، Autoencoder و شبکه‌های عصبی پیشرو برای داده‌های چند‌بعدی طراحی شده‌اند که در آن‌ها ویژگی‌ها تا حد زیادی از یکدیگر مستقل هستند. البته در شبکه‌ی کانولوشن وابستگی‌های فضایی نقاط داده مورد توجه قرار گرفته، اما در این شبکه‌ها به مولفه‌ی زمان توجه نشده است. این در حالی است که داده‌هایی مثل سری زمانی (time series)، متن و داده‌های بیولوژیکی شامل وابستگی‌های ترتیبی در بین صفاتشان هستند.

 

در سری زمانی، مقادیر مربوط به زمان‌مهر‌های متوالی ارتباط نزدیکی با هم دارند و اگر از زمان‌مهر استفاده نشود اطلاعات کلیدی در مورد روابط بین این مقادیر از بین می‌رود. در داده‌های متنی نیز اگرچه به صورت یک مجموعه از کلمات دیده می‌شوند، اما اگر ترتیب توالی کلمات را در متن در نظر بگیریم بینش منطقی بهتری بدست خواهد آمد (Aggarwal, 2018a). بسیاری از کاربردهای توالی محور (sequence-centric applications) مانند متن، اغلب به صورت کیسه‌ای از کلمات (bags of words) پردازش می‌شوند و ترتیب کلمات در متن نادیده گرفته می‌شود؛ کاربردهایی مانند classification. البته این رویکرد برای اسناد، با اندازه‌ی معقول، کار می‌کند. اما در کاربردهایی که تفسیر معنایی جمله و متن مهم باشد این رویکرد کافی نیست و حتماً باید ترتیب کلمات در متن در نظر گرفته شود؛ مانند تحلیل احساسات (sentiment analysis)، ماشین ترجمه (machine translation)، و استخراج اطلاعات (information extraction) (Aggarwal, 2018a).

از طرفی اگر برای پردازش متن یا داده‌های مشابه از یک شبکه عصبی معمولی استفاده کنیم و در آن برای هر موقعیت در دنباله، یک ورودی ایجاد نماییم، شبکه برای داده‌های با طول ثابت درست کار می‌کند. به عنوان مثال اگر پنج ورودی داشته باشیم، شبکه جملات با پنج کلمه را پردازش می‌کند اما بیش از آن را نمی‌تواند. در مواقعی هم که داده‌ی مورد نظر ما کمتر از پنج جمله باشد، ورودی مفقود خواهیم داشت. یعنی این شبکه فقط می‌تواند با داده‌های با طول پنج کلمه کار کند.

معماری‌هایی که در ابتدا نام بردیم مولفه‌ی زمان و توالی ترتیب داده‌ها را در نظر نمی‌گیرند. بنابراین نمی‌توانند وابستگی‌های زمانی حاکم در اینگونه داده‌ها را مورد پردازش قرار دهند (Aggarwal, 2018a). همچنین در این معماری‌ها اندازه‌ی ورودی ثابت است و برای داده‌های با طول متغیر کارایی ندارند.

به یک معماری شبکه عصبی نیاز است که در آن طول ورودی متغیر باشد و در عین حال پردازش ورودی‌ها در هر موقعیت و در هر زمان‌مهر به صورت مشابه انجام شود و در همان حال تعداد پارامترها نیز در آن زیاد نشود (Aggarwal, 2018a). در این معماری باید فاکتور زمان و توالی و ترتیب قرار گرفتن داده‌های ورودی در نظر گرفته شود. شبکه عصبی بازگشتی این معماری را ارائه می‌دهد و با تعداد ثابتی از پارامترها توانایی پردازش تعداد متغیری از ورودی‌ها را دارد (Aggarwal, 2018a).

در شبکه عصبی بازگشتی یک تناظر یک به یک بین لایه‌های شبکه و موقعیت‌های خاص در دنباله‌ی ورودی وجود دارد. بنابراین به جای تعداد متغیر ورودی در یک لایه، شبکه دارای تعداد متغیری از لایه‌ها است. هر لایه دارای یک ورودی منفرد مربوط به آن موقعیت یا آن زمان است. همه‌ی لایه‌ها هم از مجموعه پارامترهای یکسانی استفاده می‌کنند و به اینصورت تعداد پارامتر‌ها ثابت می‌ماند و با افزایش لایه‌ها زیاد نمی‌شود (Aggarwal, 2018a). در شبکه‌های عصبی بازگشتی مولفه‌ی زمان اهمیت زیادی دارد و این معماری‌ها برای پردازش داده‌های سری زمانی (time series) و داده‌های ترتیبی (sequential) بسیار مناسب هستند.

کاربردهای متنوعی از شبکه‌های عصبی بازگشتی وجود دارد. ورودی این شبکه‌ها به صورت دنباله‌ای از مقادیر است. در این دنباله، مقادیر منفرد می‌توانند مقادیر حقیقی باشند مانند سری زمانی یا مقادیر نمادین باشد مثل متن. شبکه عصبی بازگشتی برای هر دو به کار می‌رود. در کاربردهای عملی استفاده از آن برای مقادیر نمادین معمول است (Aggarwal, 2018a)؛ مثل داده‌های متنی.

به عنوان مثال، در یک مدل در ورودی دنباله‌ای از کلمات دریافت می‌شود و خروجی می‌تواند همان دنباله باشد که یک کلمه جابه‌جا شده است. این مدل می‌تواند برای پیش‌بینی کلمه‌ی بعدی در هر نقطه از متن مورد استفاده قرار گیرد (Aggarwal, 2018b). در مدل دیگر ورودی می‌تواند یک جمله در یک زبان و خروجی یک جمله در زبان دیگر باشد. در این مورد دو شبکه عصبی بازگشتی برای یادگیری مدل‌های ترجمه بین دو زبان به یکدیگر متصل می‌شوند. حتی می‌توان با اتصال یک شبکه عصبی بازگشتی به یک شبکه عصبی کانولوشن برای ترجمه‌ی زیر نویس تصاویر از آن استفاده کرد. در مدل دیگر ورودی می‌تواند یک دنباله از کلمات باشد، مثلاً یک جمله، و خروجی یک بردار احتمالات کلاس که در پایان جمله ایجاد می‌شود. این رویکرد برای برنامه‌های طبقه‌بندی جمله محور مانند تحلیل احساسات مفید است (Aggarwal, 2018a).

در این یادداشت کلیات معماری که در بین انواع شبکه‌های عصبی بازگشتی مشترک است مورد بررسی قرار می‌گیرند و بررسی انواع مختلف شبکه‌های عصبی بازگشتی را به سایر یادداشت‌ها موکول می‌کنیم.

با وجود اینکه تقریباً در هر حوزه‌ی دنباله‌ای (sequential) می‌توان از شبکه‌های عصبی بازگشتی استفاده کرد، از آنجایی که شبکه عصبی بازگشتی بیشتر در حوزه‌ی متن استفاده می‌شود در اینجا حوزه‌ی داده‌های متنی را برای بحث معماری این شبکه‌ها در نظر می‌گیریم. بنابراین تمرکز روی شبکه‌های بازگشتی گسسته است.

در شکل ۱ ساده‌ترین شکل از معماری یک شبکه عصبی بازگشتی نشان داده شده است. نکته‌ی کلیدی در این معماری وجود حلقه‌ی بازخورد به خود است. یک یا چند خروجی از لایه‌ی پنهان به عنوان ورودی به همان لایه وارد می‌شود. بنابراین خروجی لایه‌ی پنهان در یک زمان‌مهر به عنوان ورودی همان لایه در زمان‌مهر بعدی استفاده می‌شود. به این ترتیب حالت پنهان شبکه پس از ورود هر کلمه در دنباله تغییر می‌کند. در شکل ۲ این حلقه در لایه‌های زمانی (time-layered) باز شده است. این شکل شبیه شبکه‌های عصبی پیشرو (feedforward neural networks) است. مسلماً همانگونه که از این شکل مشخص است ماتریس‌های وزن در لایه‌های زمانی مختلف به اشتراک گذاشته شده‌اند.

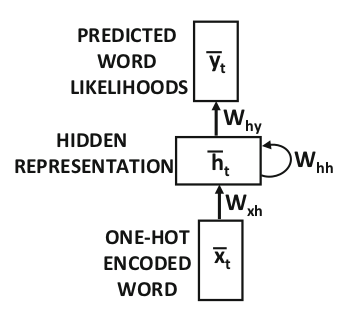
شکل ۱- معماری ساده‌ی RNN‏ (Aggarwal, 2018a)

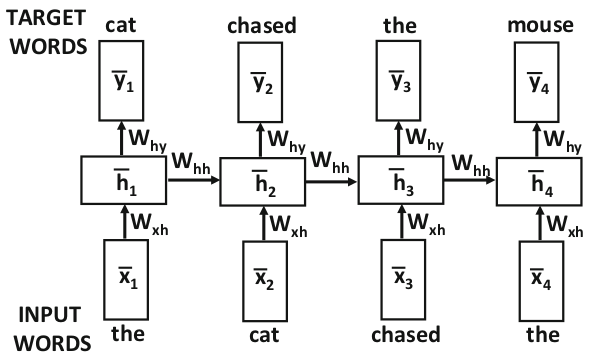
شکل ۲- نمایش لایه‌های زمانی (time-layered) شبکه‌ی شکل۱ (Aggarwal, 2018a)

در این شکل‌ها یک شبکه‌ی عصبی بازگشتی نشان داده شده که در آن هر لایه هم ورودی، هم خروجی و هم حالت پنهان دارد. اما ممکن است در یک شبکه‌ی عصبی در هر زمان‌مهر، ورودی یا خروجی نداشته باشیم. در شکل ۳ این نوع از شبکه‌ها نشان داده شده‌اند. انتخاب نوع شبکه بر اساس کاربرد مورد نظر انجام می‌شود. در این شکل به کاربردهای هر معماری نیز اشاره شده است. به عنوان مثال در کاربرد پیش‌بینی سری زمانی (time-series forecasting application) ممکن است نیاز باشد که در هر زمان‌مهر خروجی داشته باشیم تا بتوانیم مقدار بعدی سری زمانی را پیش‌بینی کنیم. از طرف دیگر در کاربرد دسته‌بندی دنباله (sequence-classification application) ممکن است که تنها یک خروجی در انتهای دنباله نیاز داشته باشیم تا کلاس آن را مشخص کنیم. معماری نشان داده شده در شکل ۱ که در شکل ۲ بسط داده شده برای مدل‌سازی زبان مناسب است. این مدل یک مفهوم شناخته شده در پردازش زبان طبیعی است که در آن کلمه‌ی بعدی در جمله پیش‌بینی می‌شود. در این معماری در هر زمان‌مهر یک کلمه از ورودی دریافت می‌شود و در خروجی کلمه‌ی بعدی را پیش‌بینی می‌کند.

ما در اینجا معماری شکل ۱ را در نظر می‌گیریم. البته به راحتی می‌توان آن را به شکل‌های دیگر تبدیل کرد. به صورت کلی در زمانt (برای کلمه‌ی tام) بردار ورودی ، بردارحالت پنهان و بردار خروجی (پیش‌بینی کلمه‌ی t+1ام) است. برای یک لغت‌نامه با اندازه‌ی d هر دو بردار و ، d بعدی هستند. بردار حالت پنهان نیز p بعدی است. همه‌ی این بردارها را ستونی در نظر می‌گیریم. بردار حالت پنهان در زمان t تابعی است از بردار ورودی زمان t و بردار پنهان زمان (t-1):

مانند همه‌ی شبکه‌های عصبی دیگر این تابع با ماتریس‌های وزن توابع فعال‌سازی (activation function) تعریف می‌شود و از یک وزن مشترک برای همه‌ی زمان‌مهر‌ها استفاده می‌کند. بنابراین با وجود تغییر حالت پنهان، وزن و تابع در گذر زمان ثابت می‌مانند. تابع گسسته‌ی برای یادگیری احتمالات خروجی از حالت‌های پنهان استفاده می‌شود.

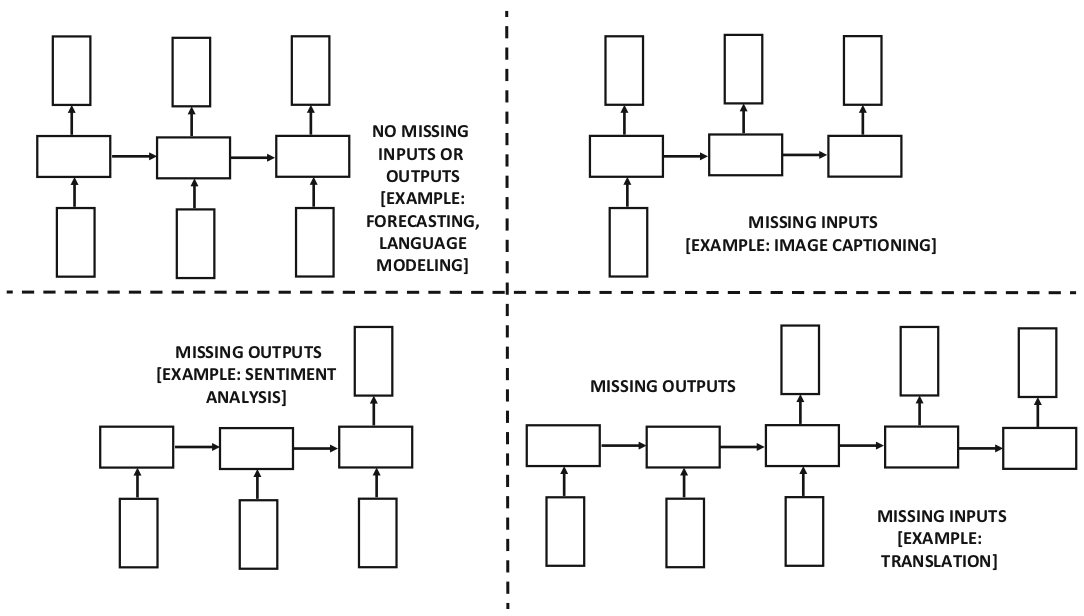
شکل ۵-۳- انواع مختلف RNN بر اساس وجود یا عدم وجود ورودی یا خروجی (Aggarwal, 2018a)

در اینجا ماتریس‌های وزن به این صورت تعریف می‌شوند. ماتریس وزن ورودی-پنهان W_xh به صورت یک ماتریس p × d، ماتریس پنهان-پنهان W_hh به صورت یک ماتریس p × p و ماتریس پنهان-خروجی W_hy به صورت یک ماتریس d × p تعریف می‌شوند. به این ترتیب رابطه‌های بالا که برای محاسبه‌ی بردار حالت پنهان و خروجی زمان t نوشته شده به صورت زیر بسط داده می‌شود:

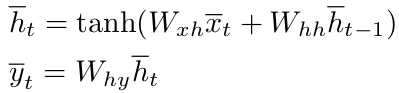
نکته‌ی جالب توجه این است که به دلیل ماهیت بازگشتی رابطه، تابع f برای ورودی‌های با طول متغیر قابل استفاده است. در‌واقع بردار حالت پنهان اول تابعی از ورودی اول است، ، و بردار حالت پنهان دوم تابعی است از ورودی اول و ورودی دوم، . به همین ترتیب بردار حالت پنهان زمان t تابعی است از ورودی‌های اول تا t‌ام. بنابراین می‌توانیم رابطه‌ی زیر را بنویسیم.

اگرچه تابع F_t نسبت به حالت بلافاصله قبلی ثابت است نسبت به زمان t تغییر می‌کند. این رویکرد برای ورودی‌های با طول متغیر مفید است. مثل جملات و کلمات که طول ثابتی ندارند.

در شبکه‌های عصبی بازگشتی وضعیت شبکه در هر واحد زمانی فقط از گذشته اطلاع دارد و از وضعیت‌های آینده هیچ اطلاعی ندارد. در برخی از کاربردها مانند مدل‌سازی زبان، با داشتن دانش در مورد وضعیت‌های گذشته و آینده، نتایج بسیار بهتری حاصل می‌شود. در شبکه‌های عصبی بازگشتی دوطرفه (Bidirectional Recurrent Networks) دو بردار حالت پنهان جداگانه برای هر زمان‌مهر داریم. بردار حالت پنهان برای حرکت رو به جلو (forward direction) و بردار حالت پنهان برای حرکت رو به عقب (backward direction). حالت‌های پنهان رو به جلو فقط با یکدیگر تعامل دارند و همین امر در مورد حالت‌های پنهان رو به عقب نیز صدق می‌کند. البته در هر دو جهت بردار ورودی یکسان دریافت می‌شود و هر دو با خروجی یکسان سروکار دارند . تنها تفاوت در جهت حرکت روی دنباله‌ی ورودی است. در شکل ۴ این معماری نشان داده شده است.

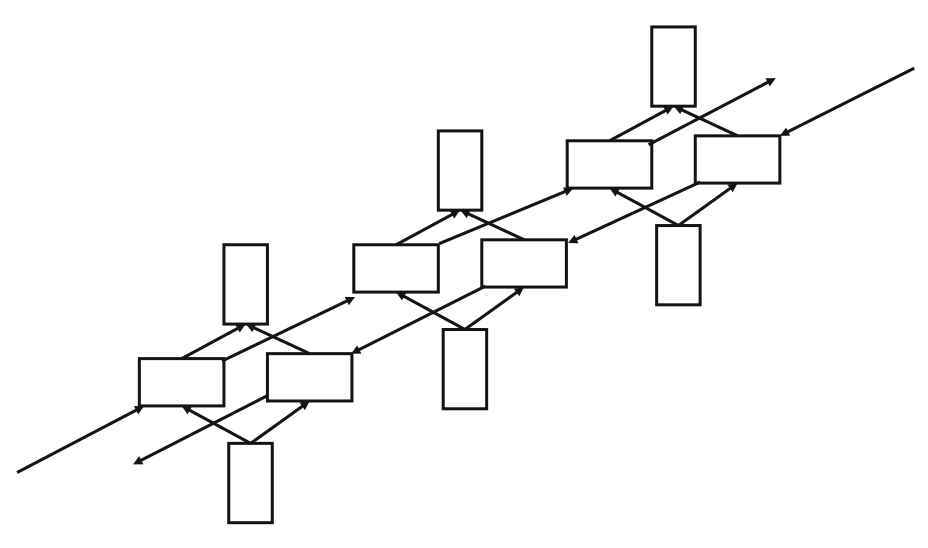
شکل ۴- نمایش لایه‌های زمانی شبکه‌ی عصبی بازگشتی دو‌طرفه (Aggarwal, 2018a)

این مدل در کاربردهایی استفاده می‌شود که سعی دارند ویژگی‌های نشانه‌های فعلی را پیش‌بینی کنند. مانند تشخیص کاراکترها در یک نمونه دست‌خط، تشخیص بخش‌های جمله در تشخیص گفتار و طبقه‌بندی نشانه‌های زبان طبیعی. از آنجایی که در این رویکرد متن از هر دو جهت پردازش می‌شود و برای نشانه یا کلمه‌ی فعلی از متن در هر دو طرف گذشته و آینده استفاده می‌شود، پیش‌بینی ویژگی‌های نشانه یا کلمه‌ی فعلی به صورت موثر‌تری انجام می‌گردد. این مسأله در پردازش زبان خیلی بیشتر دیده می‌شود و استفاده از شبکه‌های بازگشتی دوطرفه در کاربردهای مختلف زبان محور مثل تشخیص گفتار و تشخیص دست خط به صورت فزاینده‌ای رایج شده است.

در شبکه عصبی بازگشتی دوطرفه پارامتر‌های جداگانه‌ای برای حرکت‌های رو به جلو و رو به عقب در نظر گرفته می‌شود. برای حرکت رو به جلو (forward) ماتریس‌های وزن ورودی-پنهان، پنهان-پنهان و پنهان-خروجی به ترتیب ، و هستند. و به صورت مشابه برای حرکت رو به عقب (backrward) ماتریس‌های وزن ورودی-پنهان، پنهان-پنهان و پنهان-خروجی به ترتیب به صورت ، و تعریف می‌شوند. به این ترتیب حالت‌های پنهان رو به جلو و رو به عقب و خروجی برای زمان‌مهر tام به صورت زیر محاسبه می‌شوند:

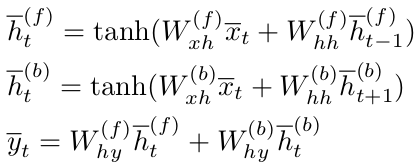
حالت‌های پنهان رو به جلو و رو به عقب با یکدیگر هیچ تعاملی ندارند. بنابراین می‌توان ابتدا برای محاسبه‌ی حالت‌های پنهان رو به جلو شبکه را به کار گرفت و پس از آن در جهت رو به عقب در دنباله‌ی ورودی حرکت کرد و حالت‌های پنهان رو به عقب را محاسبه نمود. پس از محاسبه‌ی تمام حالت‌های پنهان، خروجی‌ها قابل محاسبه خواهند بود. پس از بدست آمدن خروجی، الگوریتم پس‌انتشار برای محاسبه‌ی مشتقات جزئی دو جهت رو به جلو و رو به عقب به صورت جداگانه مورد استفاده قرار می‌گیرد. الگوریتم یادگیری که در اینجا مورد استفاده قرار می‌گیرد به نام backpropagation through time (BPTT) شناخته می‌شود.

یک شبکه عصبی بازگشتی دو طرفه تقریباً همان کیفیت نتایجی را به دست می‌آورد که با استفاده از مجموعه‌ای از دو شبکه‌ی عصبی بازگشتی جداگانه به دست می‌آید؛ در یکی از این شبکه‌ها ورودی به شکل اصلی ارائه می‌شود و در دیگری ورودی معکوس می‌شود. تفاوت اصلی این است که پارامترهای حالت‌های رو به جلو و رو به عقب به طور مشترک در شبکه‌ی عصبی بازگشتی دوطرفه آموزش داده می شوند. با این حال، این ادغام بسیار ضعیف است. زیرا این دو نوع حالت رو به جلو و رو به عقب مستقیماً با یکدیگر تعامل ندارند.

شبکه‌های عصبی بازگشتی که قبل از این مورد بررسی قرار گرفت برای سادگی به صورت تک لایه بودند. اما در عمل برای ساخت مدل‌های با پیچیدگی بیشتر لازم است که از معماری چندلایه یعنی از شبکه‌های عصبی بازگشتی چندلایه (Multilayer Recurrent Networks) استفاده شود. البته انواع مختلف شبکه‌های بازگشتی مثل LSTM و GRU را نیز می‌توان به صورت چندلایه تعریف کرد که این انواع در یادداشت‌های بعدی معرفی خواهند شد.

در شکل ۵ یک مثال از شبکه عصبی بازگشتی شامل سه لایه نشان داده شده است. در این معماری، لایه‌های سطوح بالاتر ورودی خود را از لایه‌های سطوح پایین‌تر می‌گیرند. روابط بین لایه‌های پنهان و همچنین محاسبات مربوط به حالت‌های پنهان و خروجی شبکه نیز مشابه شبکه‌ی تک لایه تعمیم می‌یابد (Aggarwal, 2018a).

رابطه‌ی بازگشتی مربوط به شبکه‌ی تک لایه را می‌توانیم به صورت زیر بازنویسی کنیم.

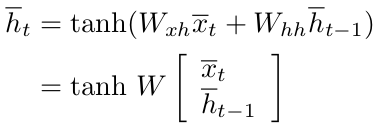
در اینجا یک ماتریس بزرگ‌تر شامل ستون‌های و استفاده شده است. به صورت مشابه ماتریس ستونی بزرگ‌تر شامل بردار حالت پنهان زمان (t-1) و بردار ورودی زمان t برای استفاده در این رابطه ساخته شده است. در شبکه‌ی عصبی بازگشتی چندلایه برای تمایز حالت‌های پنهان لایه‌های مختلف در یک زمان‌مهر از نمادگذاری استفاده می‌کنیم که بردار حالت لایه‌ی پنهان kام را در زمان t نشان می‌دهد. به صورت مشابه ماتریس وزن برای لایه‌ی kام به صورت نشان داده می‌شود. این وزن‌ها در زمان‌مهر‌های مختلف مشترک هستند ولی بین لایه‌ها به اشتراک گذاشته نمی‌شوند و هر لایه وزن مخصوص خود را دارد. ورودی هر لایه از خروجی لایه‌ی قبلی دریافت می‌شود بجز لایه‌ی اول که ورودی آن ورودی زمان‌مهر فعلی از دنباله‌ی ورودی است. بنابراین برای لایه‌ی اول محاسبه‌ی بردار حالت پنهان بر اساس رابطه‌ی زیر انجام می‌شود:

و برای لایه‌های بعدی، k≥2، از رابطه‌ی بازگشتی زیر برای محاسبه‌ی بردار حالت پنهان استفاده می‌شود:

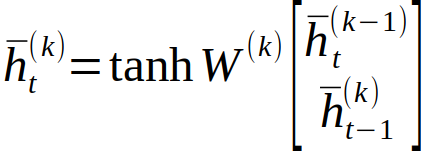
ابعاد ماتریس W⁽¹⁾ برابر است با p × (d + p) که در آن p اندازه‌ی بردار حالت پنهان و d اندازه‌ی بردار ورودی است. ابعاد ماتریس وزن W^(k) نیز برابر است با p × (p + p) = p × 2p. محاسبه‌ی خروجی از روی بردار حالت پنهان نیز به همان صورت انجام می‌شود که در شبکه‌ی تک‌لایه انجام می‌شد (Aggarwal, 2018a).

شکل ۵- شبکه‌ی عصبی بازگشتی چندلایه (Aggarwal, 2018a)

در یادداشت‌های بعدی در همین وبلاگ به معرفی انواع پر کاربرد از شبکه‌های عصبی بازگشتی خواهیم پرداخت.

منابع:

Aggarwal, C.C., 2018a. Neural Networks and Deep Learning: A Textbook. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-94463-0

Aggarwal, C.C., 2018b. Machine Learning for Text, 1st ed. 2018. ed. Springer International Publishing : Imprint: Springer, Cham. https://doi.org/10.1007/978-3-319-73531-3