شبکه عصبی بازگشتیLSTM

شبکه‌ی Long Short-Term Memory یا به اختصار LSTM، اولین بار در سال ۱۹۹۷ توسط Hochreiter و Schmidhuber معرفی شد. این شبکه اگرچه یک شبکه‌ی عصبی نسبتاً قدیمی است اما در گذر زمان میزان استفاده از آن رشد کرده و در طیف وسیعی از مسائل از آن استفاده می‌شود.

 

یک نقطه‌ی ضعف مهم در شبکه‌های عصبی بازگشتی محو شدگی گرادیان (vanishing gradients) و انفجار گرادیان (exploding gradients) است (Hochreiter et al., 2001; Larsson et al., 2016; Lawrence et al., 1997) که در عملیات به روز رسانی شبکه‌های عصبی مصنوعی شایع است. در این عملیات، مشتق‌های متوالی یا منجر می‌شوند به اینکه گرادیان بسیار کوچک و بی تأثیر شده و یا به صورت ناپایدار بسیار بزرگ شود. این نوع ناپایداری نتیجه‌ی مستقیم ضرب‌های متوالی با ماتریس وزن در زمان‌مهرهای مختلف است. در یادداشت مربوط به پرسپترون چندلایه در همین وبلاگ دیدیم که این مشکل با افزایش تعداد لایه‌ها بروز می‌کند. در شبکه عصبی بازگشتی RNN افزایش تعداد زمان‌مهرها معادل افزایش تعداد لایه‌ها در شبکه‌ی عصبی پرسپترون چندلایه است. بنابراین RNN که فقط از به روز رسانی‌‌های ضربی استفاده می‌نماید، فقط در یادگیری‌های کوتاه خوب عمل می‌کند و در یادگیری‌های طولانی با زمان‌مهر‌های زیاد عمل‌کرد ضعیفی دارد. یعنی در دنباله‌های طولانی از داده‌ها عمل‌کرد خوبی از خود نشان نمی‌دهد. به عنوان مثال در جمله‌ی «من در ایران به دنیا آمدم، کم و بیش بلد هستم که … صحبت کنم.» برای پر کردن جای خالی، کلمات همسایه کمکی نمی‌کنند. کلمه‌ی کلیدی برای پر کردن جای خالی کلمه‌ی «ایران» است که فاصله‌ی زیادی با جای خالی دارد. گرچه شبکه عصبی بازگشتی می‌تواند اطلاعات کلمات اول را به آخر متن انتقال دهد اما در عمل چنین اتفاقی نمی‌افتد. می‌توانیم بگوییم که RNN ذاتاً دارای حافظه‌ی کوتاه مدت خوب اما حافظه‌ی بلند مدت ضعیف است (Hochreiter et al., 2001) و در مواردی که فاصله‌ی داده‌های مرتبط به هم در دنباله زیاد باشد به خوبی کار نمی‌کند. این مشکل را با نام وابستگی بلندمدت یا Long Term Dependency می‌شناسیم.

یک راه حل برای رفع این مشکل، تغییر معادله‌ی بازگشتی برای بردار حالت پنهان با استفاده از حافظه‌ی بلند مدت است (Aggarwal, 2018). اساساً شبکه‌ی LSTM با همین هدف طراحی و ارائه شد. شبکه‌ی LSTM برای حل مشکل وابستگی بلندمدت یک سبد حافظه (حافظه‌ی بلندمدت) دارد و کلمات خیلی مهم را در آن نگه می‌دارد تا در جای مورد نیاز از آن استفاده کند. در ادامه‌ی مطالب، چگونگی تشکیل این حافظه و معماری LSTM را مورد بررسی قرار می‌دهیم.

معماری LSTM مانند RNN است. با این تفاوت که RNN یک ورودی و یک خروجی داشته اما LSTM دو ورودی و دو خروجی دارد. در شکل ۱ یک بلوک LSTM در مقایسه با یک بلوک RNN نشان داده شده است.

شکل ۱- مقایسه‌ی معماری RNN و LSTM (عکس‌های این یادداشت از وب سایت آکادمی هوسم گرفته شده است.)

در اینجا نیز مانند RNN بردار حالت پنهان در لایه‌ی kام در زمان‌مهر t را با نشان می‌دهیم و فرض می‌کنیم که ورودی را با نشان می‌دهیم. این معماری همان RNN چندلایه است که در یادداشت «معماری اصلی شبکه‌های عصبی بازگشتی» در همین وبلاگ در مورد آن صحبت کردیم. اما در اینجا رابطه‌ی مربوط به محاسبه‌ی متفاوت است. برای این منظور یک بردار پنهان اضافی در نظر گرفته شده که به صورت نشان داده می‌شود. C اول cell State یا حالت سلول است و می‌توان آن را نوعی حافظه‌ی بلندمدت (Long Term Memory) دانست. C_t-1 مستقیماً به C_t وصل است. بنابراین حالت‌های سلول‌ها یک خط ورودی-خروجی را تشکیل می‌دهند که از ابتدا تا انتهای بلوک‌های زمانی LSTM به هم وصل هستند و در گذر زمان در آن اطلاعاتی ذخیره شده و یا از آن حذف می‌شود. به این ترتیب حداقل بخشی از اطلاعات قبلی با عملگر‌های فراموشی (forgetting) و افزودن (increment) درحافظه‌ی بلند‌مدت حفظ می‌شود (Aggarwal, 2018). در شکل ۲ این عملگر‌ها نشان داده شده‌اند.

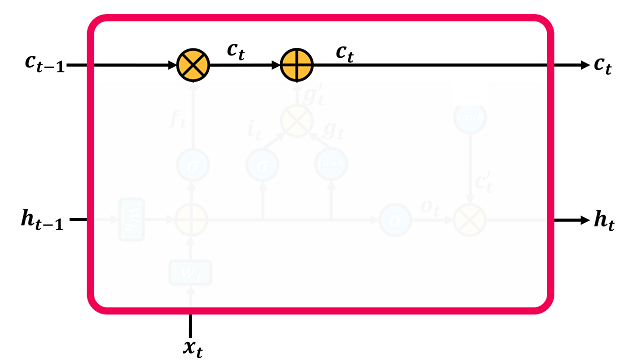
شکل ۲- عملگرهای فراموشی و افزودن در معماری LSTM

در شکل ۲ عملگر فراموشی (forgetting) با علامت × نشان داده شده است. این عملگر دو ورودی دارد. یکی و یکی دیگر هم است که از داخل بلوک LSTM می‌آید. طول هر دو بردار یکسان است و f_t قبل از این از تابع سیگموید گذشته است بنابراین مقادیر این بردار عدد‌هایی در بازه‌‌ی [1 ,0] هستند. عملگر فراموشی این دو بردار را به صورت درایه به درایه ضرب می‌کند (element-wise product) و خروجی آن یک بردار با همان‌طول اولیه‌ی بردار‌ها است. هرجا درایه‌ای در بردار f صفر باشد مانع عبور درایه‌ی مربوطه در بردار C_t-1 و انتقال آن به C_t می‌شود. اگر درایه‌‌ای در بردار f یک باشد یعنی درایه‌ی مربوطه در بردار C_t-1 بدون تغییربه بردار C_t عبور کند. اگر هم درایه‌ی بردار f مقداری بین صفر و یک داشته باشد معنی آن این است که درایه‌ی مربوطه در بردار C_t-1 تا حدودی تغییر کرده و سپس به بردار C_t منتقل می‌شود. به این ترتیب با این عملگر می‌توان اطلاعاتی را از C که همان حافظه‌ی بلند‌مدت شبکه است حذف کرد.

یکی از ورودی‌های مورد نیاز برای اجرای این عملگر f_t است که با یک شبکه عصبی کوچک از نوع پرسپترون چندلایه به نام دروازه‌ی فراموشی (forget gate) بدست می‌آید. در شکل ۳ این دروازه نشان داده شده است.

شکل ۳- دروازه‌ی فراموشی

نحوه‌ی محاسبه‌ی f برای زمانی که شبکه یک لایه دارد در شکل ۴ نشان داده شده است.

شکل ۴- نحوه‌ی ماسبه‌ی مقدار f

زمانی که شبکه چندین لایه داشته باشد رابطه‌ی مربوط به محاسبه‌ی f در زمان‌مهر t برای لایه‌ی kام به صورت زیر است.

در این رابطه W_hf ماتریس وزن مربوط به حالت پنهان (h) در دروازه‌ی فراموشی (f) است. W_if ماتریس وزن مربوط به ورودی (i) در دروازه‌ی فراموشی (f) است. به صورت مشابه b_hf و b_if نیز نشان دهنده‌ی مقادیر بایاس مربوط به حالت پنهان (h) و ورودی (i) در دروازه‌ی فراموشی (f) هستند.

در شکل ۲ عملگر افزودن (increment) با علامت + نشان داده شده است. این عملگر کار اضافه کردن اطلاعات جدید به حافظه‌ی بلندمدت C را انجام می‌دهد. قبل از اجرای این عملگر باید به این سؤال پاسخ داده شود که چه اطلاعاتی را می‌خواهیم به حافظه‌ی بلندمدت اضافه کنیم. پاسخ این است که مشابه عملگر ضرب با یک شبکه عصبی MLP محاسبه می‌شود. در شکل ۵ نحوه‌ی محاسبه‌ی بردار g_t (مقداری که باید به حافظه‌ی بلندمدت اضافه شود) در حالتی که شبکه یک لایه دارد نشان داده شده است. به دلیل استفاده از تابع تانژانت هایپربولیک، g مقادیری در بازه‌ی [1 ,1-] دارد. به این ترتیب برخی از درایه‌های بردار C را کاهش و برخی را افزایش می‌دهد.

البته در این شکل به نظر می‌رسد که این وزن‌ها با وزن‌های دروازه‌ی فراموشی یکی باشد که البته اینطور نیست و در پایین شکل توضیحاتی در این زمینه نوشته شده است.

زمانی که شبکه چندین لایه داشته باشد رابطه‌ی مربوط به محاسبه‌ی g در زمان‌مهر t برای لایه‌ی kام به صورت زیر خواهد بود.

در این رابطه W_hg ماتریس وزن مربوط به حالت پنهان (h) برای محاسبه‌ی g است و W_ig نیز ماتریس وزن مربوط به ورودی (i) برای محاسبه‌ی g می‌باشد. به صورت مشابه b_hg و b_ig نیز نشان دهنده‌ی مقادیر بایاس مربوط به حالت پنهان (h) و ورودی (i) برای محاسبه‌ی g هستند.

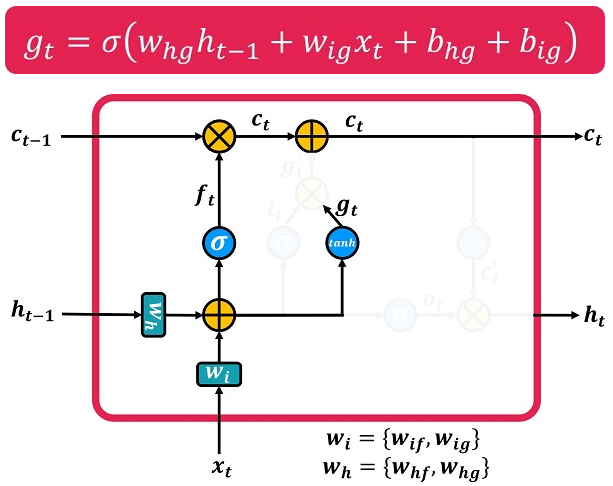
شکل ۵- محاسبه‌ی بردار g

به ترتیبی که در بالا گفته شد اطلاعاتی که در زمان t بدست آورده‌ایم، یعنی g_t، محاسبه می‌شود. اما این اطلاعات چقدر اهمیت دارد؟ و آیا باید آن را در حافظه‌ی بلندمدت، C_t، ذخیره کنیم یا نه؟ برای پاسخ به این سؤال از روشی مشابه دروازه‌ی فراموشی استفاده می‌کنیم که به آن دروازه‌ی ورودی می‌گوییم. در شکل ۶ دروازه‌ی ورودی و نحوه‌ی انجام محاسبات مربوط به آن، در حالتی که شبکه یک لایه دارد نشان داده شده است.

زمانی که شبکه چندین لایه داشته باشد رابطه‌ی مربوط به محاسبه‌ی i در زمان‌مهر t برای لایه‌ی kام و همچنین روش اعمال آن در حافظه‌ به صورت زیر است.

در این رابطه‌ها W_hi ماتریس وزن مربوط به حالت پنهان (h) در دروازه‌ی ورودی (i) است. W_ii ماتریس وزن مربوط به ورودی (i) در دروازه‌ی ورودی (i) است و به صورت مشابه b_hi و b_ii نیز نشان دهنده‌ی مقادیر بایاس مربوط به حالت پنهان (h) و ورودی (i) در دروازه‌ی ورودی (i) هستند.

شکل ۶- دروازه‌ی ورودی و محاسبات مربوط به آن

تا اینجا دیدیم که چگونه بر اساس مقادیر بدست آمده در هر بلوک، اطلاعات در حافظه‌ی بلند مدت C، ثبت و یا از آن حذف می‌شود. اما در نهایت قرار است در جایی از این حافظه‌ استفاده شود و آنچه که در بلوک‌های زمانی قبلی به خاطر سپرده شده در خروجی نهایی هر بلوک زمانی تاثیرگذار باشد. سؤال این است که چگونه از حافظه‌ی C برای محاسبه‌ی خروجی استفاده می‌کنیم. مطمئناً تمام اطلاعات موجود در آن مورد استفاده قرار نمی‌گیرد؛ بلکه فقط بخشی از آن استفاده می‌شود. این کار با دروازه‌ی خروجی انجام می‌شود. دروازه‌ی خروجی مشخص می‌کند که چقدر از حافظه‌ی بلند مدت باید به خروجی منتقل شود. در شکل ۷ بلوک LSTM به صورت کامل نشان داده شده است. در این شکل نسبت به شکل ۶، در مرحله‌ی آخر، برای محاسبه‌ی h_t دروازه‌ی خروجی اضافه شده است. در این شکل رابطه‌ی مربوط به محاسبه‌ی خروجی، برای حالتی که شبکه یک لایه دارد نیز نشان داده شده است.

زمانی که شبکه چندین لایه داشته باشد رابطه‌ی مربوط به محاسبه‌ی خروجی h در زمان‌مهر t برای لایه‌ی kام به صورت زیر است.

در این رابطه‌ها W_ho ماتریس وزن مربوط به حالت پنهان (h) در دروازه‌ی خروجی (o) بوده و W_io نیز ماتریس وزن مربوط به ورودی (i) در دروازه‌ی خروجی (o) است. به صورت مشابه b_ho و b_io نیز نشان دهنده‌ی مقادیر بایاس مربوط به حالت پنهان (h) و ورودی (i) در دروازه‌ی خروجی (o) هستند.

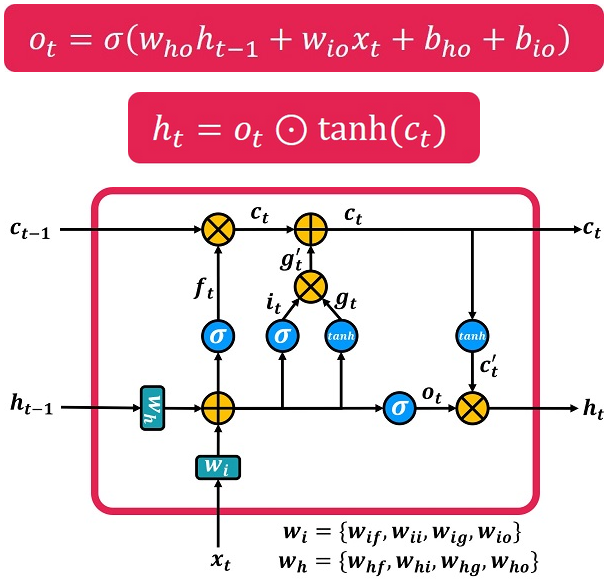
شکل ۷- معماری کامل یک بلوک LSTM

منابع:

Aggarwal, C.C., 2018. Neural Networks and Deep Learning: A Textbook. Springer International Publishing, Cham. https://doi.org/10.1007/978-3-319-94463-0

Hochreiter, S., Bengio, Y., Frasconi, P., Schmidhuber, J., 2001. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. A field guide to dynamical recurrent neural networks. IEEE Press In.

Larsson, G., Maire, M., Shakhnarovich, G., 2016. FractalNet: Ultra-Deep Neural Networks without Residuals. https://doi.org/10.48550/ARXIV.1605.07648

Lawrence, S., Giles, C.L., Ah Chung Tsoi, Back, A.D., 1997. Face recognition: a convolutional neural-network approach. IEEE Trans. Neural Netw. 8, 98–113. https://doi.org/10.1109/72.554195